Calculer l’aire d’un triangle rectangle

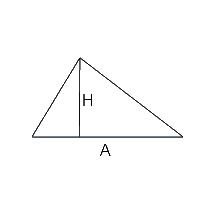
L’aire du triangle rectangle

Calculez l’aire d’un triangle rectangle de façon rapide en posant une formule simple : Aire = (base x hauteur) / 2. La base et la hauteur sont les côtés qui forment l’angle droit. Attention, le triangle peut aussi être présenté avec la base sur le dessus, car tout dépend de l’angle droit.

Cette formule ressemble beaucoup à celle du calcul de l’aire d’un rectangle (l’aire d’un rectangle étant définie par base x hauteur) car comme nous l’avons vu précédemment, le triangle rectangle représente exactement la moitié d’un rectangle. C’est donc la même opération que pour l’aire d’un rectangle, puis l’on divise par deux.

Le triangle dans tous ses états

Le triangle se divise en plusieurs catégories définies par ses angles ou par la longueur de ses côtés. Le triangle isocèle a pour caractéristique de posséder deux côtés de même longueur. Contrairement au triangle rectangle, il ne possède pas d’angle droit. S’il en possède un, il devient alors un triangle rectangle avant d’être un triangle isocèle. Pour calculer son aire, il suffit de le diviser en deux triangles rectangles en faisant partir un segment à angle droit depuis sa base jusqu’à son sommet. L’on obtient alors deux triangles auxquels on applique la formule vue précédemment pour calculer l’aire exacte de la surface. Ceci nous donne comme formule : A = [(base 1 x hauteur 1) / 2] + [(base 2 x hauteur 2) / 2]. Il en va de même pour le triangle équilatéral qui possède trois côtés identiques, ainsi que pour le triangle quelconque qui n’est doté d’aucune particularité. Tous les triangles peuvent ainsi être divisés en deux triangles rectangles.

La définition du triangle

Le triangle est défini par le principe de géométrie euclidienne comme une figure plane, dotée de trois sommets par trois segments qui les joint. Ces segments sont appelés côtés.

Obtusangle et acutangle

Le triangle acutangle est défini par la taille de ses angles dont aucun ne dépasse les 90°. Ce sont des angles que l’on appelle aigus. En revanche, le triangle obtusangle possède un angle supérieur à 90°. C’est un angle que l’on nomme obtus. Un triangle rectangle ne peut par définition pas posséder d’angle obtus, car il est doté d’un angle droit et deux angles aigus. Il en va de même pour le triangle équilatéral, qui de ses trois côtés identiques ne peut faire surgir un angle obtus. A noter qu’un triangle ne peut jamais comporter plus d’un angle obtus. Enfin, dans tous les cas, qu’il s’agisse d’un triangle obtusangle ou d’un triangle acutangle, la somme des trois angles d’un triangle est toujours égale à 180°, du moment qu’il s’agit de géométrie euclidienne qui est enseignée dans les matières scolaires de base. En géométrie elliptique ou hyperbolique, l’on peut trouver des triangles dont les sommes des angles sont supérieures à 180°, mais ce sont là des méthodes plus complexes. La géométrie elliptique définit qu’étant donnés un segment et un point extérieur à ce segment, il n’existe aucun segment parallèle passant par ce point.

Le théorème de Pythagore

Bête noire des élèves qui débutent un apprentissage approfondi de la géométrie, le théorème de Pythagore qui doit être appris par cœur est pourtant un allié afin de définir les longueurs des côtés d’un triangle. Plus précisément, le théorème de Pythagore s’applique aux triangles rectangles pour qui il observe que le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés. Ainsi, l’on peut calculer l’une des longueurs du triangle rectangle en fonction des deux autres. Pour un triangle rectangle dont l’on nomme les côtés A, B et C, cela donne la formule : A² + B² = C².